数学の世界観2(初等数学)
数学の世界観2(初等数学)です。
初等・中等数学
初等数学の基本
初等数学、すなわち算数については、算術と幾何学に分けて考える必要があります。
算術について言えば、四則演算と累乗、平方根の考え方を知っておくことです。
まず、プラスとマイナスがあること、すなわち、加法と減法があり、減法はマイナスをつけた加法によって成り立つことをまず知っておきましょう。
次に、乗法と除法がありますが、これは分数として分子と分母で表すことができます。乗法は分子で、除法は分母で成り立つことを知っておきましょう。
また、マイナスとマイナスをかければプラスになるという事実と、分母の違う分数は同じ分母に通分することで計算できることを知っておきましょう。
同時に、分数は小数点を用いることで、小数で表すこともできると知っておきましょう。
小学校ならば、ここまでで十分ですが、中学以降では、まず、文字式の考え方で、未知数を方程式を使って、移項して解く方法、それから関数とグラフ(座標とX軸・Y軸)の考え方、比例と反比例の考え方を知っておきましょう。
また、累乗の考え方、すなわち、同じ数だけ掛け算を行うのを、指数すなわち次元として捉えること、累乗の逆の方法として、それを二乗するとその数になる平方根の考え方を、必ず覚えておきましょう。
最後に、幾何学の問題として、四角形や三角形やさまざまな図形(ひし形、台形など)の面積を出す方法、角、辺、直角、平行、直線、点などの考え方と、円周率\(\pi\)を用いた円の円周の長さや面積を出す方法を必ず覚えておいてください。
三角形としては、一般の三角形のほかに、二等辺三角形や直角三角形があります。また、三次元の立体についても知っておいてください。
また、もっとも使える小学校の算数の知識は、九九の計算方法と、繰り上がりのある足し算や引き算、あるいは桁の多い掛け算や割り算のために必要となる、筆算を書く方法です。
これらの知識を、必ず覚えておいてください。これくらいが分かっていれば、高校は難しくありません。基礎がしっかりしている人は、応用もそつなくこなすことができるからです。
小学校算数の背後にある考え方
以下に、学校で習った小学校の算数を、大人になって反省する必要がでてきた人向けに、素晴らしい書籍を紹介する。
この書籍は、小学校でなんとなく習った算数の知識を、「何をどのように教えているのか」「自分は何を教わったのか」ということをもう一度知ることのできるいい本である。
算数的な考え方
単に「数学的に考える」と言っても、小中学校の算数や数学を覚えていないわたしたち大人は、どのようなことを考えればいいか分かりません。
なので、グラムやメートルといった単位や、三角形や四角形のような面積しか、数学的なことを思いつかない、という風になってしまいます。
ですが、小中学校の算数や初等数学は、「入門算数学」を読むとよく分かります。
初等数学において言えることは、「四則演算と数量」「図形と面積」「文字式とグラフ」に分けるとよく分かります。
まず、すべての前提として、10進法(十進位取り記数法)で数を表しますが、情報などでは2進数や16進数が使われることもあります。
数学の基本は四則演算です。四則演算とは、足し算、引き算、掛け算、割り算のことです。これに加えて、累乗、有理数である分数や小数の演算、そして無理数、あるいはさらに虚数が加わります。
図形と面積については、直線と辺と角、平行、そして三角形や四角形や円が加わります。さらに、円周率、平方根、立体、合同と相似が加わります。これらについて、面積と体積を求めます。
文字式とグラフは、文字を使った計算です。文字式の基本は方程式と関数です。初等的な関数のグラフには正比例(1次関数、グラフが直線となる)や反比例(双曲線)などがあります。そして、数の関係性について、割合、確率、統計が求められます。
初等数学において、主に登場するのはこれらの考え方です。
さらに中学校以降では、2次方程式や2次関数(放物線)が登場します。また、高校では解の公式、三角比や三角関数、微分積分、指数対数やネイピア数、ベクトルと行列などが登場します。
これらについて、ひとつひとつの計算のルールを覚えて、さまざまな問題から正しい解答を導きます。また、値を求めるための計算だけではなく、論理が正しいことを証明するために証明も行います。
これらの考え方を一般化したものを、「数学的な考え方」と呼ぶのです。
このように見ると、基本的に出てくるのは、比率あるいは割り算であるということが分かります。基本的に、数学では四則演算を中心に考えますが、有理数の主役となるのは割り算です。ほかの多くの計算も、多くが有理数的な「比率」をベースとしています。分数・有理数の英語訳はRationalであり、比率の英語訳はratioです。なので、比率が分かれば初等数学はできます。
(入門算数学を参考に執筆しました。)
2025.06.10
2025.06.16編集
初等数学の基本
九九の表
1~10×1~10:
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
1~10×11~20:
| × | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
11~20×11~20:
| × | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
2026.01.31
分数の計算
分数の計算について。
割り算や循環小数は分数として表すことができる。たとえば、
\[ 2 \div 3 = \frac{2}{3} = 0.66666 \cdots = 0.\dot{6} \]
分数は、分子と分母に同じ数を掛けても値は変わらない。
\[ 2 \div 3 = \frac{2}{3} = \frac{4}{6} = \frac{6}{9} \]
分数同士の足し算は、分母を通分することで行うことができる。通分とは、足し算をしたい分数同士が同じ分母になるように、分数の分子と分母に同じ数の掛け算をして、分母をそろえること。
たとえば、
\[ \frac{1}{2} + \frac{5}{4} = \frac{1 \times 2}{2 \times 2} + \frac{5}{4} = \frac{2}{4} + \frac{5}{4} = \frac{7}{4} \]
あるいは、
\[ \frac{1}{2} + \frac{2}{3} = \frac{1 \times 3}{2 \times 3} + \frac{2 \times 2}{3 \times 2} = \frac{3}{6} + \frac{4}{6} = \frac{7}{6} \]
となる。
また、分数同士の掛け算は、それぞれの分子と分母同士の掛け算になる。小さくできる場合、数はできるだけ小さいほうがいい。
\[ \frac{4}{3} \times \frac{1}{2} = \frac{4 \times 1}{3 \times 2} = \frac{4}{6} = \frac{2}{3} \]
また、分数の割り算をする時には、分子と分母を逆にした数(逆数)を掛ける。
\[ \frac{1}{2} \div \frac{1}{3} = \frac{1}{2} \times \frac{3}{1} = \frac{1 \times 3}{2 \times 1} = \frac{3}{2} \]
それから、分数は小数に直すことができる。この場合は通常の割り算と同じように筆算などを使って計算すればいい。
\[ \frac{1}{2} = 1 \div 2 = 0.5 \]
割り算のルールとして、数を0で割ってはならないのと同様に、分数の分母を0にすることはできない(ただし、無限に0に近くすることはできる)。
分数で表すことのできる数のことを有理数と呼ぶ。無理数が発見されるまで、数学には有理数しか存在しないと考えられていた。かつてのピタゴラスは無理数の存在をかたくなに否定した。
- 【高校数学Ⅰ】「循環小数1(分数→循環小数)」 | 映像授業のTry IT (トライイット)
- tmt's mathemaTeX page! - 0.4 循環小数の秘密
- 循環小数 - Wikipedia
2025.01.25
円
これに対して、円周率\(\pi\)のような無理数は分数に表すことができない。
\[ \pi = 3.14159 \ 26535 \ 89793 \ 23846 \cdots \]
\(\pi\)の値はこれ以後無限に続き、循環小数のように循環しない。
円周の長さと円の面積は、rを円の半径とした時、円周の長さは\(2 \pi r\)、円の面積は\(\pi r^2\)で求められる。
2025.01.25
三角形
また、三角形の面積は、小学校で習ったように「底辺×高さ×2分の1」で計算できるが、三角形の2辺(bとc)とその間の角(A)が分かっていた場合、三角比を使って、
\[ S = \frac{1}{2} bc \sin A \]
でも求めることができる。
2辺であれば、cとaの組み合わせと角Bであっても、aとbの組み合わせと角Cであっても成り立つため、
\[ S = \frac{1}{2} bc \sin A = \frac{1}{2} ca \sin B = \frac{1}{2} ab \sin C \]
となる。
また、三角形の1辺とその両端の角が分かっている場合は、
\[ S = \frac{a^2 \sin B \sin C}{2 \sin (B+C)} \]
となる。
そして、三角形の3辺が分かっている場合は、
\[ S = \sqrt{s(s-a)(s-b)(s-c)} \quad ただし \ s=\frac{a+b+c}{2} \]
となる。最後の式をヘロンの公式と呼ぶ。
- 図解入門よくわかる高校数学の基本と仕組み
- 基礎からのシグマベスト 高校 これでわかる数学I+A(文英堂, 2008年発行版)
2026.02.04
円錐、球、円柱の体積
円に関連する体積について、球の半径をrとした時、同じ高さ(2r)の円錐の体積は\(\frac{2}{3} \pi r^3\)、球の体積は\(\frac{4}{3} \pi r^3\)、円柱の体積は\(2 \pi r^3\)になる。
これを比にすると、円錐:球:円柱=1:2:3となる。発見したアルキメデスの墓にも彫られていたとされる有名な比である。
(入門算数学を参考に執筆しました。)
2025.01.28-29
関数と放物線
中学数学では、さまざまな関数のグラフについて学ぶ。
たとえば、一次関数・正比例(直線)、反比例(双曲線)、二次関数(放物線)。
このうち、放物線とは、ものを斜め上へと放り投げた時に、そのものが軌跡として描く方向を書いたものである。
以下はgnuplotで描いた\(y = 2x\)のグラフ(一次関数・正比例)。
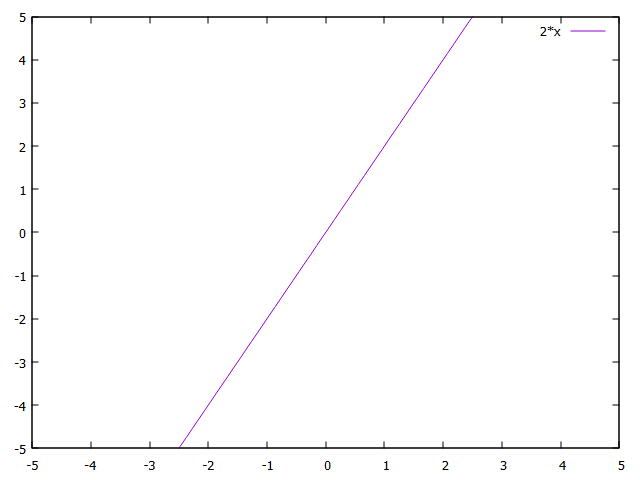
以下はgnuplotで描いた\(y = \frac{2}{x}\)のグラフ(反比例)。
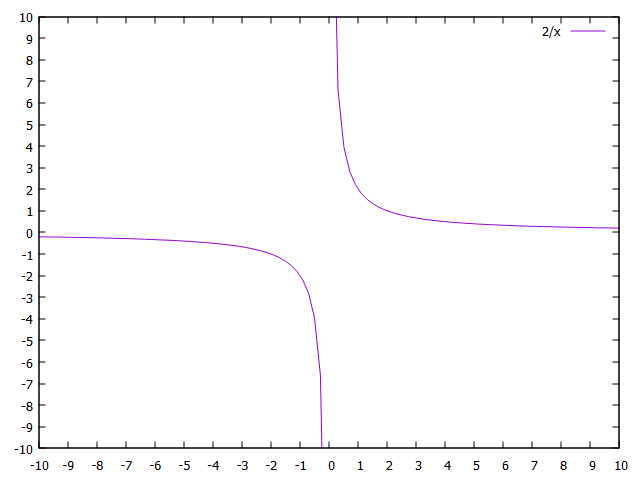
以下はgnuplotで描いた\(y = x^2\)のグラフ(二次関数)。
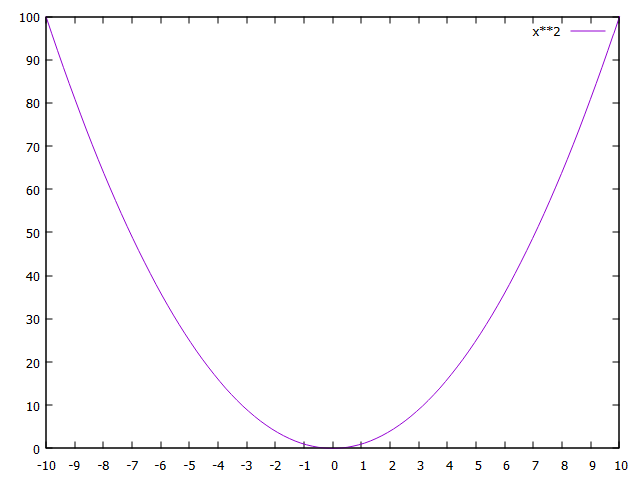
(「シグマベスト これでわかる数学 中学三年 (2008年発行版)」を参考に執筆しました。)
2026.01.24
2026.02.26-27編集
連立方程式
方程式には、通常のひとつの式の移項によってひとつの文字の値を解く一元方程式のほかに、複数の式を組み合わせて、複数の文字の値を計算することによって解く「連立方程式」がある。
連立方程式の解き方には、加減して文字を消去する「加減法」と、代入して文字を消去する「代入法」がある。
2026.01.24
合同と相似
合同とは、互いにぴったり重ね合わされる図形のこと。合同な図形においては、対応する辺と角の大きさは等しい。
相似とは、ある図形を一定の割合で拡大縮小した図形のこと。相似な図形においては、対応する辺の比率と、角の大きさは等しい。
2026.02.09
さまざまなこと
数学の基本は算術と幾何学
僕は、数学の基本は算術と幾何学だと思います。
算術とは、足し算、引き算、掛け算、割り算のような、数に対する計算の数学です。
これに対して、幾何学とは、直線、円、三角形、角度、辺、面積、などなどのような、図形に対する法則の数学です。
たとえば古代ギリシャでは、算術と幾何学は別々の独立した学問でした。算術は算術、幾何学は幾何学という風に、別々に教えられていたのです。
それが、デカルトによる解析幾何学によって、方程式を幾何学で表したり、幾何学を方程式に表したりするようになりました。
デカルトが馬鹿だと言うつもりはありません。ですが、数学の基本はいつであっても、算術と幾何学だと僕は思います。
中学校の数学から、算数は数学になり、方程式や代数、関数やグラフなどを中心とした数学になります。幾何学についても、文字式を使った幾何学になります。
ですが、小学校の数学では、算術と幾何学をそれぞれ、個別に扱うことができます。
僕は、こうした小学校の数学のように、算術と幾何学を別々に扱うことで、基本的な「数学的論理の意味」が把握できることもあると思います。
デカルト以降の近代数学をたしなむ前に、このような古代の数学、算術と幾何学を別々に扱う数学を学ぶことで、数学の基礎を掴むことはとても有益だと思います。
なので、小学校の算数は、馬鹿にはできない「基本の本来あるべき数学」だと僕は思います。
子供に数学を教えるためには、数学は数の学問であると教えるべき
子供に算数や数学を教える時に重要なのは、「数学は数の学問」だと教えることです。
たとえば、子供に引き算を教える時、15-8=7となるのを、子供に計算しやすく教えるために、15-10+2=7であると教えることがあります。
このような「数の取り替え」が成り立つのは、数学が数の学問だからです。
数学は数の学問であり、「式には値がある」ということが重要です。式には値があり、値が変わらない限りにおいて、式のどんな数を変更しても構いません。左式と右式が等しい場合においては、どのように数を取り替えても、式を追加しても構わないのです。
ですが、小学校で算数を習っている子供は、そうした数学は数の学問であるということを知りません。なので、15から先に10を引いて2を足すという発想が分からず、「どうしてそんなことをしていいのか」が分からないのです。
よって、小学生に算数を教える時は、「数学は数の学問」であり、「数の学問だから好きなように数を取り替えて計算していいのだ」ということを教えることが大切です。ここが分かるかどうかで、算数が得意になるか、あるいは数学が好きになるかどうかが分かれてくると思います。
中学数学が知性である所以
中学数学は、つまらない当たり前で単純な基礎数学だと思っているかもしれない。そう考える大人が多い。
だが、僕の経験からするに、中学数学はとても大きな「知性」の身につく、良い数学である。
ネットゲームをするのであっても、あるいは社会に出て自分の力でこの世界を経験的・根源的に考える上でも、中学数学の知性は役に立つ。
中学数学の知性があれば、大人よりも賢い「哲学者」になれる。
だが、中学数学は、中学2年ぐらいで終わってしまい、中学3年ぐらいから、「高校数学の準備」のようなものが始まってしまう。
数学が嫌われるのは、その高校数学のせいである。高校数学は、逆に、知性が無くなって、考えられなくなってしまうのである。
中学数学の知性があると良い点として、「自分で科学を作れる」ということが言える。そう、中学数学ができてしまうと、教師に習わなくても、自分で大学の資料を調べて、自分でいくらでも独自の数学や科学を作れるようになる。昔の自分は、まさにそういう人間だった。高校で馬鹿になるのは、高校数学をやるとそういう「考える数学」がなくなってしまう。何も考えなくなって、常識と引き換えに知性を失う。それが、高校の数学である。
本当の理想は、むしろ、中学生になった段階ですぐに大学生と同じことをやること。大学に入れなくても、自分で独自にインターネットを見て、独自に研究することはできる。高校が必ずしも間違っているわけではない。指数・対数や三角関数、微積分のような考え方は、大学の物理学や情報理論・コンピュータアーキテクチャなどを学ぶ上で、いくらでも出てくる。それらを本当に理解したいなら、高校には行くべきである。
高校・大学の数学は、考えない方ができる
中学生が数学をすると、考えることが多い。たくさんの考えることに初めて触れることで、考えれば考えるほど、数学が好きになる。
それは、中学数学は、純粋な考え方を身につけることを目的にしているからである。
だが、高校に入ると、逆に、高校数学に挫折する人間が多い。これは、高校の数学は、中学のように、「考えることではできない」からである。
中学生は、ネットゲームをやらせても、カードゲームをやらせても、いつでも考える。考えれば考えるほど、新しいことが分かる。
だが、高校では、考えることではできない。つまり、「高校・大学の数学は、考えない方ができる」のである。
高校や大学では、定理と証明を暗記し、いくら定理を覚えているかで点が決まる。彼らは考えていない。考えないで、どんどん知るだけで、高校の数学はできてしまう。
だが、それは高校や大学の数学が間違っている、ということではない。高校で習う指数・対数や三角関数や微分積分学は、必ず大学やパソコンの習得にも役に立つ、とても有用的で便利な数学理論である。それらを身につけたいのであれば、中学とはやり方を変えること。中学では「当たり前に考えるだけでできた」ことも、高校では通用しない。高校の数学は、考えない方ができる。
余談
日本人が数学ができないのは、いちたすいちはにという日本語のせい
僕は、日本人が数学ができないのは、「1 + 1 = 2」を「いちたすいちはに」と言ってしまう日本語のせいだと思います。
日本人は、=の表現に「は」を使ったため、1 + 1と2が同じものだと勘違いしています。「同じ」であるということが強調され、「1 + 1によって2が作り出される」ということが無視されてしまっているのです。
1 + 1は確かに2かもしれませんが、たとえば0 + 2も2であるように、1 + 1だけが2であるわけではありません。1 + 1という演算を行って、その結果1 + 1に等しい2という数が「生み出される」という視点が重要なのです。
たとえば、英語では「one plus one equals two」となります。フランス語では「un plus un font deux」となります。
僕は、日本語の「いちたすいちはに」という表現は間違っていると思います。より正しい日本語として、「いちたすいちでに」にしてはどうでしょうか。「は」を「で」に変えるだけですが、このほうが明らかに数学的に正しいと思います。
日本は基礎研究を疎かにしすぎた
日本人が数学ができないことの理由に、「基礎研究を疎かにしすぎた」ということがあると思います。
日本の政府は、自動車や家電製品のような、すぐに使えて儲かるような応用技術には多くの予算を与え、投資をしてきましたが、すぐには儲からないような「基礎研究」にはお金を与えてきませんでした。
そのため、基礎研究の塊であるような、基礎の数学や物理学の研究が置き去りにされてしまい、結果、日本には数学者が少なくなってしまったのです。
この結果、数学だけではなく、ソフトウェアやコンピュータ科学においても、基礎研究が置き去りにされた結果、アメリカの大学のようなソフトウェアの高度な技術が育たなかったのです。
そのため、日本のIT技術は完全に遅れています。数学ができないということが、日本のIT技術の進歩を妨げたと言えます。
小学校の教え方は賢い
僕が思ったこととして、「小学校の教え方は賢い」ということが言える。
まず、足し算を覚えて、二つの数の加算ができるようになる。
そして、この覚えた足し算を使って、そのまま掛け算と九九を覚える。
この掛け算で、面積の計算や、分数の計算ができるようになる。
このように、小学校の算数は、「一度覚えたことをさらに活用して新しいことを覚える」ということを繰り返していき、最終的に積み重ねる。
そう、僕に足りないのは、まさにそのような「覚えて使う」という行為だ。
昔の僕は、常に覚える人間だったし、覚えたことを常に活用する人間だった。
いつからか、僕は何も覚えることなく、覚えたことを活用することもない人間になった。
だが、小学校の算数のような「積み重ね」が、過去の高校時代の「僕の独自の経験的な数学」を作り上げた。
もう一度、まず単純に覚えて、その覚えたことをさらに使って別のことを覚える、ということをすれば、僕はきちんと日本語も分かるようになるし、精神も楽になるだろう。
2023.08.14
足し算と掛け算の違い
足し算と掛け算の違いについて。
足し算とは、「数の目盛りが1ずつ増えていく」ということです。
すなわち、10進法であれば10分の1である「1」という単位を目盛りとして、1ずつ数を増やしていくこと、これが足し算です。
これに対して、掛け算とは、「数の比率の単位を倍にする」ということです。
すなわち、全体が10だったものに10を掛けて100にするのであれば、10という比率の単位を10倍にして、比率におけるひとつ当たりの大きさを拡大するのです。
なので、基本的に、目盛りと比率によって四則演算は成り立っていると言えます。
2025.06.10
賢くなりたいなら、中学二年の数学をやれ
僕が分かったこと、それは、「賢くなりたいなら中学二年の数学をやれ」ということです。
中学数学をやる理由、それは考える訓練になるからです。
中学校の数学は、「正しく考えれば分かる」という特徴があります。これに対して、高校の数学は「一部の天才以外には考えても分からない」という特徴があります。
そして、小学校の算数は、具体的な計算をやっているだけで、頑張っても計算のスピードが速くなるだけで、賢くはなりません。
中学の数学をやると、自分でこの世界を考えて、計算式を解いたり論理的に証明したりすることができるようになります。
それに対して、高校数学は頭が馬鹿になります。それは一部の天才以外には考えても何のことやらさっぱり分からないため、考えることをやめてしまい、試験のために公式を覚えるだけになるからです。
そして、中学数学の中でも、中学二年をやるべきです。まず、中学一年については、計算のための基本的な規則しか分かりません。中学二年では、定理と証明を用いたり、連立方程式や一次関数の難しい問題を解いたり、図形の性質や確率の基本を学びます。そのため、中学二年の数学をやることこそが、真に正しく賢くなる方法です。
そして、中学三年は、逆にしなくて構いません。まず、僕は中学三年の始めに学校を不登校になったので、僕自身も中学三年の数学はしていませんが、それとは裏腹に、このホームページに書かれている内容は、中学三年以降の数学について書きました。なので、逆に、中学三年ぐらいから、最近の僕と同じになってしまい、知性を失って馬鹿になります。それは僕にとって「昔の自分」ではなく、「最近の自分」をやっているからです。なので、簡単に言えば、中学二年までが昔の僕で、中学三年以降が今の僕だと言えます。
なので、今の僕のように、知性を失って馬鹿になりたくないのであれば、中学二年で数学の勉強を終わりにし、あとは昔のように自分の人生経験から考えるべきなのです。それを「哲学者」と呼びます。
2025.10.11
関連ページ
数学について
関連する日記
2024-10-08に関連する内容があります。