指数対数の世界観
指数対数の世界観です。
指数関数
指数関数と底
指数関数は\(y=a^x\)となる式のことで、\(a\)を「底(てい)」と言う。英語では底のことを「base」という。
たとえば、
\[y=2^x\]
の時は、2倍ずつどんどん値が増えていく。逆に、
\[y = \bigg(\frac{1}{4}\bigg)^x\]
の時は、どんどん値が\(\frac{1}{4}\)になっていく。
とても大きな増え方をするので指数関数は「驚異的な関数」として知られている。
- 指数関数 - 自然科学のための数学I/II(2016年度)- 琉球大学
- 指数関数とは?1分でわかる意味、公式、底、計算とグラフの関係 - 建築学生が学ぶ「構造力学」
- 図解入門よくわかる高校数学の基本と仕組み
2023.11.16
2026.01.31編集
指数法則の拡張
指数関数は、\(y=a^x\)という式になります。
しかしながら、指数であるxがマイナスの場合はどうなるでしょうか。
yはxの関数であるため、このグラフを書くと、必ずどこかに答えとなる数が存在することになります。
しかしながら、「aをマイナス回数かける」というのは、あまりに非現実的です。
しかしながら、xがプラスの時は、xが増えるにしたがってyはa倍されていき、xが減るにしたがって\(\frac{1}{a}\)倍されていきます。
それならば、マイナスになるに従い、\(\frac{1}{a}\)倍されていくと考えるのが必然的です。
このように、「都合のいいように指数関数を定義する」ことを、指数関数の拡張といいます。
また、指数xが分数の場合はどうでしょうか。これを二乗すると、
\[(a^{\frac{1}{2}})^2=a^{(\frac{1}{2}) \times 2}=a\]
となります。二乗すればaになるのだから、これを\(\sqrt{a}\)と定義するのです。そして同様に、三乗根、四乗根となっていきます。
このように、「自然な見た目になるように拡張」していくのです。
(詳しくは図解入門よくわかる高校数学の基本と仕組みが参考になります。)
指数関数のグラフ
以下はgnuplotで描いた\(y = 2^x\)のグラフ。
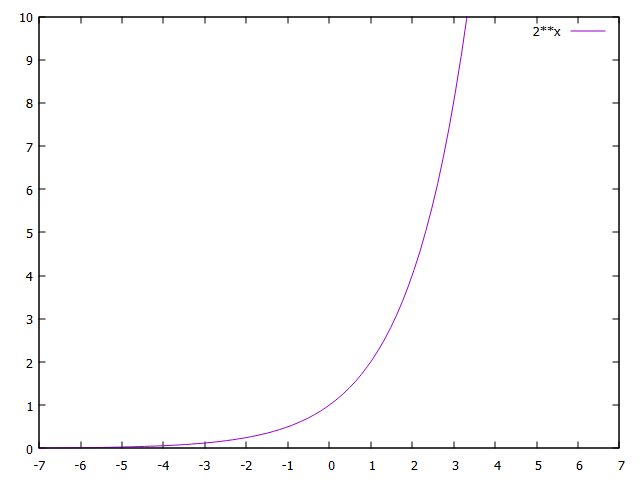
2026.02.26-27
連分数
連分数
連分数とは、分数の分母の中に分数が続いていくような分数のこと。
\[ x = a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cfrac{1}{a_3+\cfrac{1}{a_4+\cfrac{1}{a_5}}}}} \]
ただし、このように書くのは面倒なため、+記号を下に下げて記述する表記法もある。
\[ x=a_0 +\frac{1}{a_1} \lower 0.7em{+} \frac{1}{a_2} \lower 0.7em{+} \frac{1}{a_3} \lower 0.7em{+} \frac{1}{a_4} \lower 0.7em{+} \frac{1}{a_5} \]
また、分子がすべて1である場合、簡略化した記法として、
\[ [a_0; a_1, a_2, a_3, a_4, a_5] \]
と表記する。
(以上は「現代数学への入門 代数入門 (上野健爾 岩波書店)」を参考に執筆しました。)
2024.07.20-21
2026.01.31編集
黄金数
連分数についての例として、黄金数を挙げる。
黄金比(黄金数)は、
\[ \varphi = \frac{1 + \sqrt{5}}{2} \]
で示される比のことで、二次方程式の\(x^2 - x - 1 = 0\)の解として求められるが、これを
\[ x = 1 + \frac{1}{x} \]
と変形する。xについての解は求められる形にはなっておらず、左辺を求めようとすると右辺に全体の式が紛れ込み、xは無限に繰り返される。
\[ \varphi = 1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{\ddots}}}}} \]
これを黄金数の連分数表示と呼ぶ。
以下はラマヌジャンによる黄金数\(\varphi\)、円周率\(\pi\)、ネイピア数\(e\)の繋がったとても興味深い公式。
\[ \cfrac{1}{1 + \cfrac{e^{-2\pi}}{1 + \cfrac{e^{-4\pi}}{1 + \cfrac{e^{-6\pi}}{1 + \cfrac{e^{-8\pi}}{\ddots}}}}} = \big( \sqrt{2 + \varphi} - \varphi \big) e^{2\pi/5} \]
(オイラーの贈物を参考に執筆・引用しました。)
2024.07.21
平方根・無理数
平方根と有理化
累乗と一緒にセットで教えられることの多い平方根。たとえば\(\sqrt 2\)は2乗すると2になる数のことを表す。
たとえば\(\sqrt 2\)は、分数や循環小数にならないために無理数と呼ばれる。
\[ \sqrt 2 = 1.41421 \ 35623 \ 73095 \ 04880 \cdots \]
昔はこの「無理数」の存在を認めない数学者(たとえばピタゴラスで、数はすべて比によって表すことのできる有理数であると主張した)が多く、多くの議論の的だった。
有理化とは、数を無理数から有理数に変換すること。特に、分数の分母に無理数が存在する場合、分母から無理数を取り除くことを「分母の有理化」と呼ぶ。
\[ \frac{1}{\sqrt{2}} = \frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2} \]
- 有理化とは?やり方を分かりやすく解説!練習問題つき|高校生向け受験応援メディア「受験のミカタ」
- 第7回 ルートの有理化 | 数学I | NHK高校講座テレビ学習メモ
- 平方・平方根の表 - 安房高等学校パソコン部
- 平方根|有理化とは?|中学数学|定期テスト対策サイト - Benesse
2024.02.24
2026.01.31編集
2026.02.04編集
平方根とπの連分数展開
\(\sqrt{2}\)のような無理数は、有理数の極限として表現できる。以下は連分数による\(\sqrt{2}\)の展開。
\[ \sqrt{2} = [1; \overline{2}] = 1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{\ddots}}}}}} \]
このように、平方根は必ず、循環連分数となる。このことを上手く使うことで、たとえば第6近似の
\[ \sqrt{2} \fallingdotseq 1+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2+\cfrac{1}{2}}}}} = \frac{99}{70} = 1.14142857 \cdots \]
を求めるなどして、\(\sqrt{2}\)の近似値を求められる。
同様に、
\[ \sqrt{3} = [1; \overline{1, 2}] = 1+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1+\cfrac{1}{\ddots}}}}}} \\ \sqrt{5} = [2; \overline{4}] = 2+\cfrac{1}{4+\cfrac{1}{4+\cfrac{1}{4+\cfrac{1}{4+\cfrac{1}{4+\cfrac{1}{\ddots}}}}}} \\ \sqrt{7} = [2; \overline{1, 1, 1, 4}] = 2+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{4+\cfrac{1}{1+\cfrac{1}{\ddots}}}}}} \]
となる。
同様に、\(\pi\)も連分数展開できる。
\[ \pi = 3+\cfrac{1^2}{6+\cfrac{3^2}{6+\cfrac{5^2}{6+\cfrac{7^2}{6+\cfrac{9^2}{6+\cfrac{11^2}{\ddots}}}}}} \\ \frac{4}{\pi} = 1+\cfrac{1^2}{3+\cfrac{2^2}{5+\cfrac{3^2}{7+\cfrac{4^2}{9+\cfrac{5^2}{11+\cfrac{6^2}{\ddots}}}}}} \]
\(\pi\)は超越数であるため、正則連分数展開(分子がすべて1)には規則性はないが、正則でない連分数展開(上記)には規則性があるものがある。
2026.01.31
対数関数
対数関数
対数関数\(c = \log_{a}b\)は「aのc乗でbになる」という意味で、\(a\)を底、\(b\)を真数と呼ぶ。つまり、
\[c=\log_{a}b \\ a^c=b\]
を意味する。
これをやっていると、たとえば「2を何乗すると7になるか」とか、対数でなければ表現できない「そんな数が本当にあるの?」と言うことがある。
しかしながら、実数であるためグラフのどこかに必ず対応する場所が存在する。
そのため、logを用いてこの数を表すことができる。
(詳しくは図解入門よくわかる高校数学の基本と仕組みが参考になります。)
2023.11.16編集
2026.01.31編集
自然対数と常用対数
自然対数は\(\log_{e}x\)と書き、自然対数の底であるeのことをネイピア数と言う。
また、\(\log_{e}x\)は微分すると\(\frac{1}{x}\)になる。\(\log_{e}x\)のことを\(\ln{x}\)とも書く。
微分方程式や複利計算など、数学の多くの場面でネイピア数eを使うことがある。
eはπと同様の無限小数が続く無理数である。
\[ e = 2.71828 \ 18284 \ 59045 \ 23536 \ \cdots \]
また、10を底とする対数\(\log_{10}x\)のことを常用対数と言う。
また、指数関数\(e^x\)のことを\(\exp(x)\)と書く。
以上は以下のページを参考に執筆しました。
- 自然対数・常用対数・二進対数の使い分け。log,ln,lg,expはどういう意味?|アタリマエ!
- 自然対数の底(ネイピア数) e の定義と覚え方。金利とクジの当選確率から分かるその使い道|アタリマエ!
- ネイピア数とは|自然対数の底eについて解説 - 空間情報クラブ|株式会社インフォマティクス
オイラーも参照のこと。
2026.01.31編集
ネイピア数eの定義
自然対数の底であるネイピア数eは以下のように定義される。
\[e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} + \cdots\]
右辺の数列の項は無限に続き(無限級数)、この総和をeとする。
n!はnの階乗を表す。
\[5! = 5 \times 4 \times 3 \times 2 \times 1 = 120\]
あるいは、以下のようにも定義できる。
\[e = \lim_{n \to \infty}\bigg(1 + \frac{1}{n}\bigg)^n\]
円周率πや虚数単位iと同様、ネイピア数eは数学において非常に重要な数である。
以上は以下の書籍・ページを参考に執筆しました。
2023.02.22
ボルツマンの原理と統計学
統計力学の重要な公式であるエントロピーについてのボルツマンの原理については、熱力学を参照のこと。
また、統計学については統計も参照のこと。
logは指数を求める
(以下の文章は、logや対数について何も分かっていない、常識のない自分の書いた文章であるため、一般的な良識と比較して間違ったことを教えています。注意してご覧ください。)
logは難しいと思う方が多いですが、基本的に「指数を求める」ものであると考えれば分かりやすいです。
\(\log_{10}\)という「約束事」が決められた場合に、その数がどれほどの指数で表すことができるか、という関数が対数関数です。
対数で複雑な計算をする
対数を使うことで、巨大な数に対する複雑な計算が簡単にできます。
古くから、そろばん(アバカス)やアルゴリズムなどを計算に使っていた歴史上の算術計算で、比較的新しい方法として考え出されたのが、対数を使った計算です。
対数では、数の掛け算や割り算を、対数の足し算や引き算に変換することができます。
二つの数の掛け算をしたければ、まず対数表で対数を探し、その対数を足した上で、その結果に対して対数表で真数を探します。割り算ならば対数を引きます。累乗ならば対数を掛けます。平方根のような根の計算であれば対数を割ります。
この対数による計算は、巨大な数の複雑な計算をする上で計算するのを簡単にしてくれます。対数を使った計算尺などは、コンピュータが生まれた今でもまだ使われています。
また、対数について、10を底とする常用対数は、コンピュータの登場によってあまり使われなくなりましたが、eを底とする自然対数は今でも多くの科学者の間で使われています。
(ザ・ストーリー 数学大図鑑を参考に執筆しました。)
2023.02.22
1増えると10倍になる
対数による数値計算の基本は、「1増えると10倍になる」ということ。5が6になるだけで、数が10倍になる。計算尺においては、1つ目盛りが増えると数が10倍になる。
2023.02.22